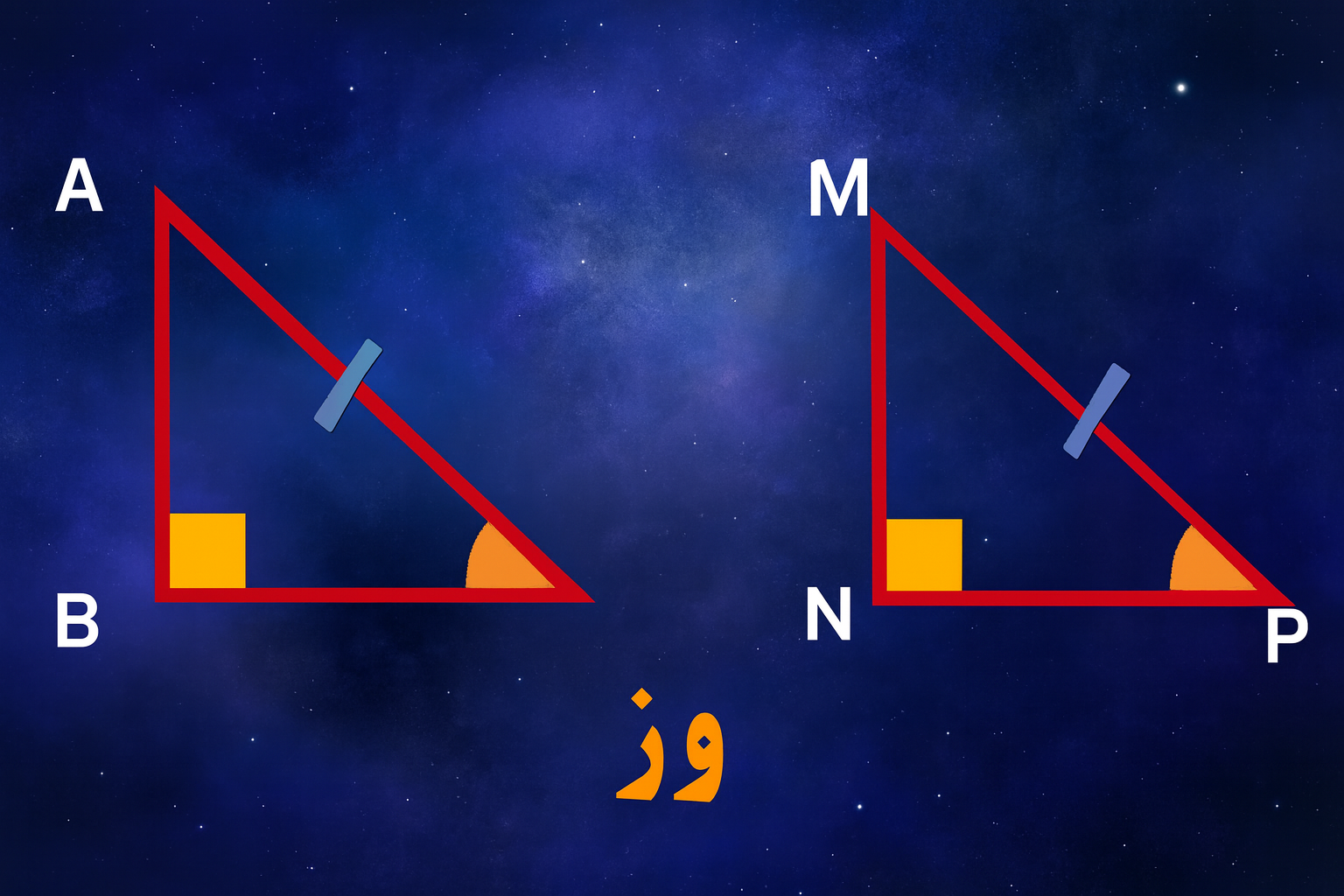
قضیه وتر وزاویه
قضیهٔ «وتر و زاویه» یکی از قضیههای همنهشتی در مثلثهای قائمالزاویه است. طبق این قضیه، اگر در دو مثلث قائمالزاویه، وترها با هم برابر باشند و یکی از زاویههای تند آنها نیز با هم برابر باشد، آن دو مثلث همنهشتاند. همانطور که مشخص است، این قضیه فقط برای مثلثهای قائمالزاویه کاربرد دارد. وجود زاویهٔ قائمه که در هر دو مثلث برابر و ثابت است، نقش مهمی در این قضیه دارد. وقتی وتر و یک زاویهٔ تند مشخص باشد، شکل مثلث کاملاً تعیین میشود. در این حالت دیگر امکان رسم مثلث متفاوتی با این شرایط وجود ندارد. بنابراین میتوان نتیجه گرفت که دو مثلث دقیقاً روی هم منطبق میشوند. این قضیه در حل مسائل زاویهدار بسیار کمککننده است.

ریشه و کاربرد آن
قضیهٔ وتر و زاویه در واقع ترکیبی از دانستن طول و زاویه است و از نظر مفهومی به سایر حالتهای همنهشتی مرتبط میشود. این قضیه نیز ریشه در هندسهٔ کلاسیک یونان دارد و مفاهیم آن در آثار اقلیدس دیده میشود. از این قضیه در مسائل اثباتی و محاسبهٔ اندازهٔ اضلاع و زاویهها استفادهٔ زیادی میشود. در طراحی سازهها، شیب سقفها و حتی در محاسبات فنی ساده میتوان ردپای آن را دید. نکتهٔ جالب این است که این قضیه نشان میدهد گاهی دانستن یک زاویه، به اندازهٔ دانستن یک ضلع مهم است. این موضوع به درک عمیقتر رابطهٔ بین طولها و زاویهها کمک میکند. به همین دلیل، قضیهٔ وتر و زاویه یکی از قضیههای مکمل و کاربردی در مبحث همنهشتی مثلثها بهشمار میآید
