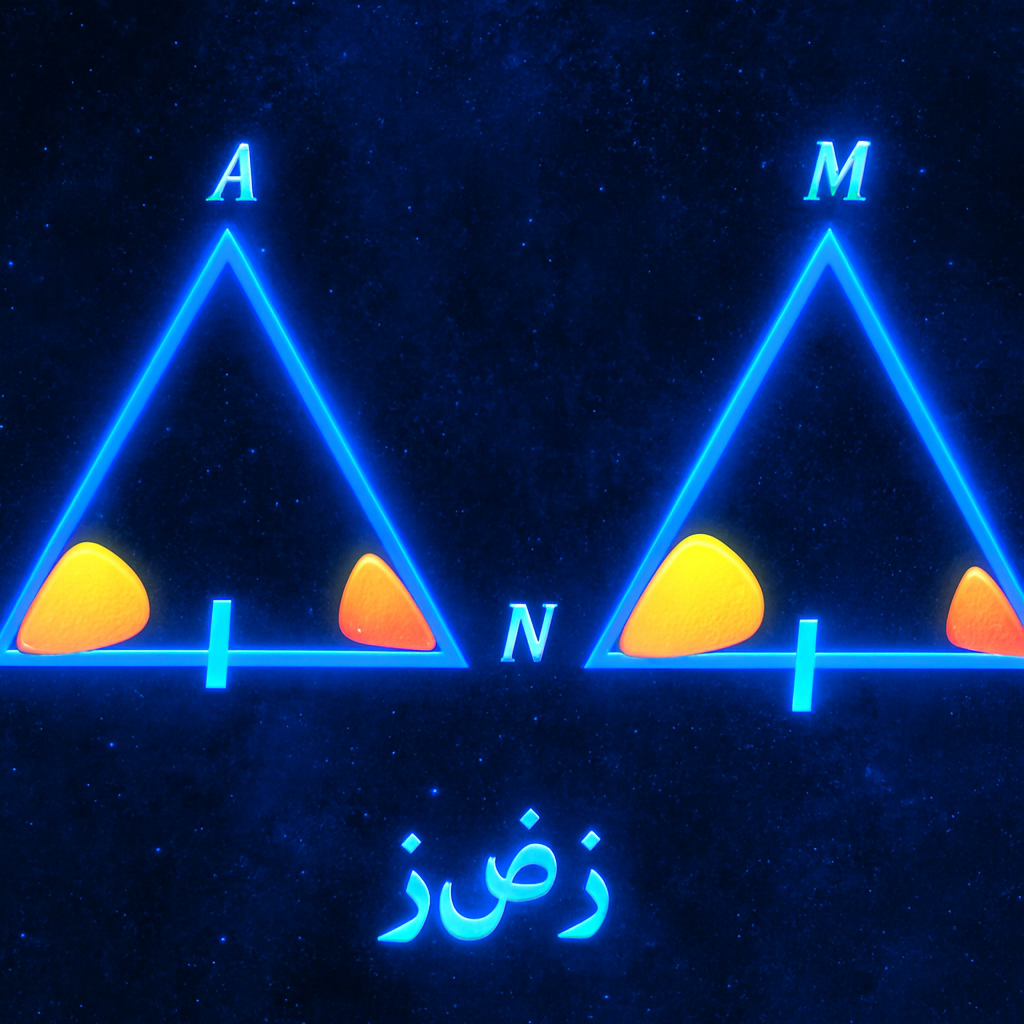
قضیه زضز / زاویه، ضلع، زاویه
قضیهٔ زضز یکی از حالتهای همنهشتی مثلثهاست که میگوید اگر در دو مثلث، دو زاویه و ضلعِ بین آن دو زاویه با هم برابر باشند، آن دو مثلث همنهشتاند. تأکید مهم این قضیه روی «ضلعِ بین دو زاویه» است، چون اگر ضلع بین آنها نباشد، ممکن است مثلثها همنهشت نشوند. وقتی دو زاویهٔ یک مثلث مشخص باشد، زاویهٔ سوم هم بهطور خودکار مشخص میشود. حالا اگر ضلع بین آن دو زاویه هم برابر باشد، شکل مثلث کاملاً تعیین میشود. در این حالت هیچ مثلث متفاوتی با این شرایط نمیتوان رسم کرد.
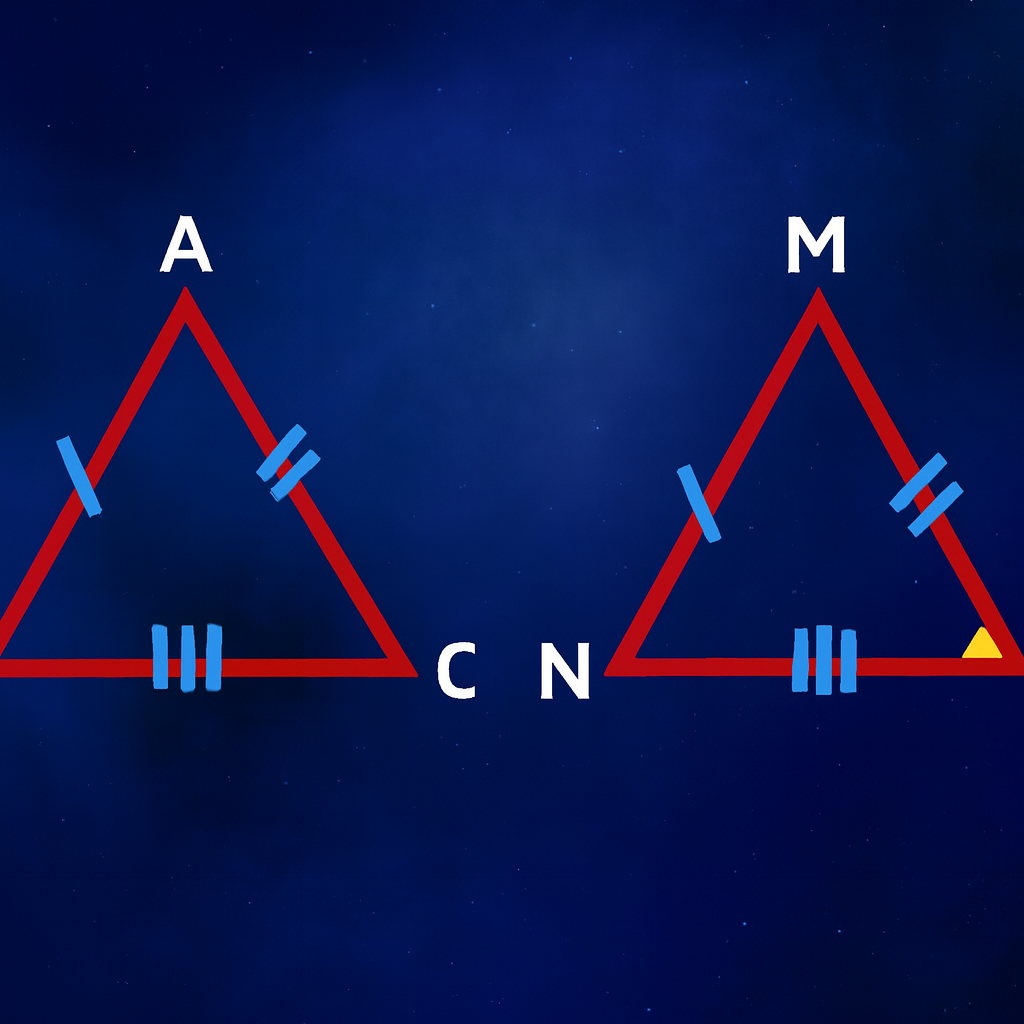
قضیه ضضض / ضلع، ضلع، ضلع
قضیهٔ ضضض سادهترین و شهودیترین حالت همنهشتی مثلثهاست. طبق این قضیه، اگر سه ضلع یک مثلث با سه ضلع مثلث دیگر برابر باشند، آن دو مثلث همنهشتاند. دلیل این موضوع این است که اضلاع، اسکلت اصلی مثلث را تشکیل میدهند. وقتی طول هر سه ضلع مشخص باشد، هیچ آزادیای برای تغییر شکل مثلث باقی نمیماند. البته باید توجه داشت که این اضلاع باید بتوانند یک مثلث بسازند (یعنی مجموع دو ضلع از سومی بزرگتر باشد). این قضیه پایهٔ بسیاری از استدلالهای هندسی است.
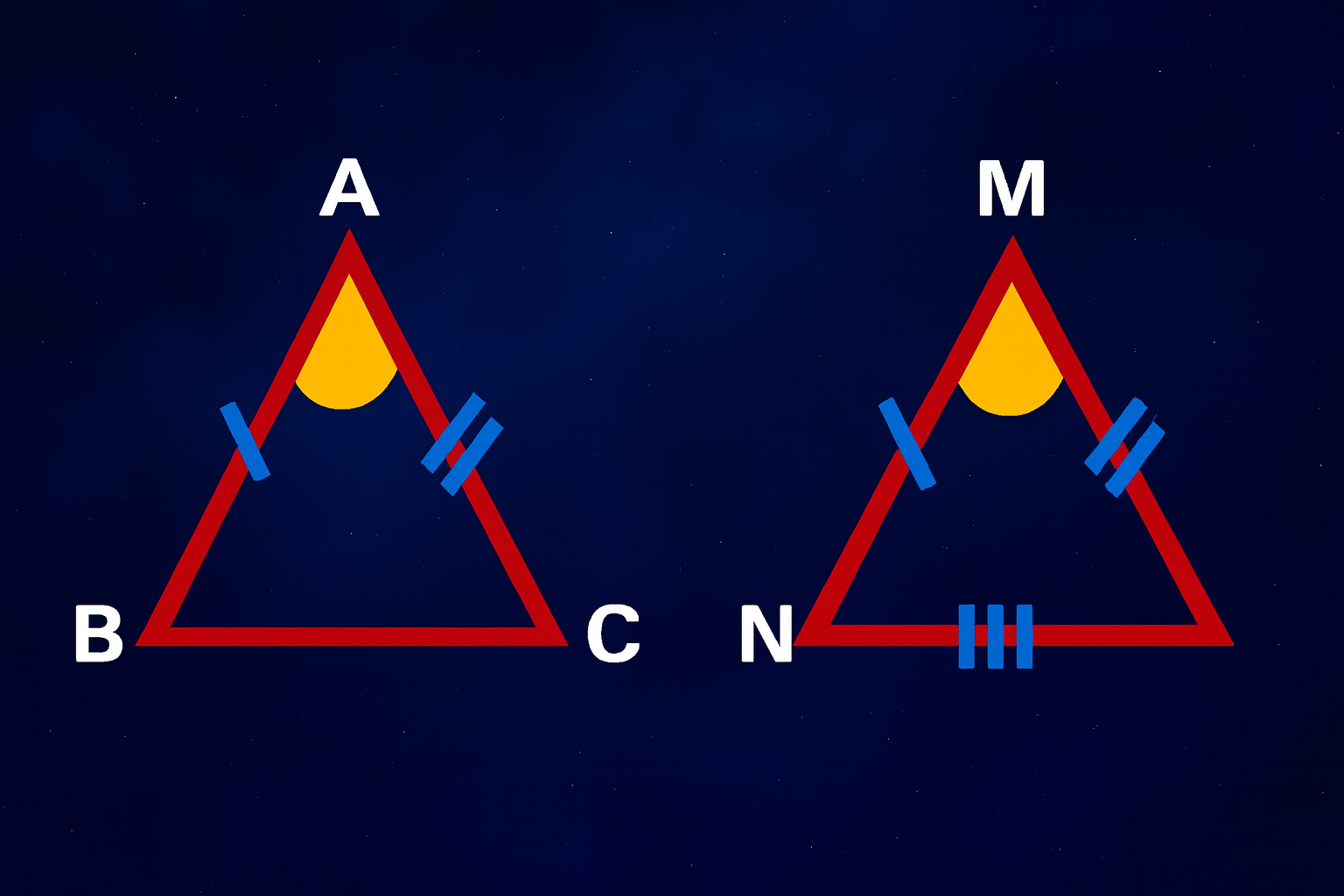
قضیه ضزض / ضلع، زاویه، ضلع
قضیهٔ ضزض بیان میکند اگر در دو مثلث، دو ضلع و زاویهٔ بین آنها با هم برابر باشند، آن دو مثلث همنهشتاند. در این قضیه هم مانند زضز، «بین بودن زاویه» اهمیت زیادی دارد. اگر زاویه بین دو ضلع نباشد، ممکن است دو مثلث متفاوت تشکیل شود. این قضیه در واقع ترکیبی از اطلاعات طول و زاویه است. وقتی دو ضلع و زاویهٔ بینشان مشخص باشد، محل ضلع سوم کاملاً تعیین میشود. بنابراین فقط یک مثلث میتوان با این شرایط رسم کرد.

ریشه و کاربرد این قضایا
این سه قضیه همنهشتی از زمان یونان باستان شناخته شده بودند و بهصورت منظم در کتاب «اصول» اقلیدس مطرح شدند. اقلیدس از این قضیهها برای اثبات بسیاری از نتایج هندسی استفاده کرد. در واقع این قضیهها ابزار اصلی هندسهٔ کلاسیک هستند. در معماری، نقشهکشی، مهندسی و حتی طراحی پلها از همین قضایا استفاده میشود. جالب است بدانید که نجاران و بنّاهای قدیم، بدون دانستن نام این قضیهها، بهصورت تجربی از آنها بهره میبردند. این قضیهها نشان میدهند که برای شناخت یک شکل، همیشه لازم نیست همه چیز را بدانیم. دانستن اطلاعات «کلیدی» کافی است. یادگیری این مفاهیم قدرت استدلال و دقت ذهن را بهطور چشمگیری افزایش میدهد.
