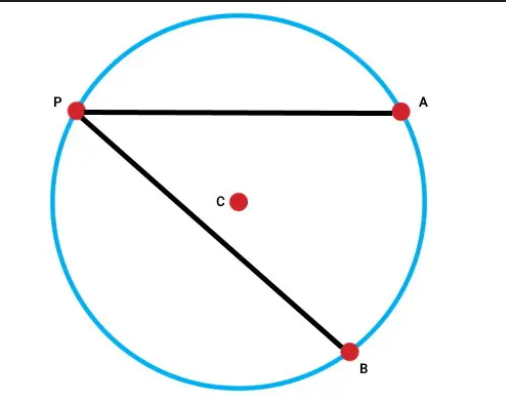
زاویه های محاطی
قضیهٔ زاویههای محاطی یکی از مهمترین و پرکاربردترین قضیهها در هندسهٔ دایره است. طبق این قضیه، اندازهٔ هر زاویهٔ محاطی برابر است با نصف اندازهٔ کمانی که آن زاویه مقابل آن قرار دارد. زاویهٔ محاطی زاویهای است که رأس آن روی محیط دایره قرار گرفته و دو ضلع آن، دو وتر دایره را تشکیل میدهند. برای درک بهتر این قضیه، کافی است دایرهای رسم کنیم و دو نقطه روی محیط آن انتخاب کنیم و آنها را به نقطهای دیگر روی محیط وصل کنیم. در این حالت زاویهای که تشکیل میشود، زاویهٔ محاطی نام دارد. این قضیه به ما اجازه میدهد بدون استفاده از ابزار اندازهگیری، اندازهٔ زاویهها را بهصورت دقیق محاسبه کنیم. همچنین در بسیاری از مسائل، با دانستن اندازهٔ یک زاویهٔ محاطی میتوان اندازهٔ کمان یا زاویههای دیگر را بهسادگی به دست آورد.
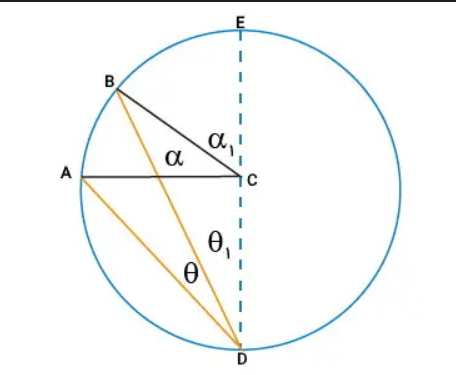
ریشه و کاربرد این قضیه
ریشهٔ این قضیه به هندسهٔ یونان باستان بازمیگردد و برای نخستین بار بهصورت منظم در کتاب «اصول» اثر اقلیدس مطرح شده است. گفته میشود یونانیان باستان با مشاهدهٔ حرکت خورشید و ستارگان به روابط دایرهای علاقهمند شدند. داستان جالبی وجود دارد که دریانوردان قدیم از این روابط هندسی برای جهتیابی استفاده میکردند. زاویههای محاطی به آنها کمک میکرد موقعیت خود را نسبت به ستارگان تشخیص دهند. این نشان میدهد که هندسه تنها یک علم نظری نبوده، بلکه کاربردهای عملی فراوانی داشته است. امروزه نیز این قضیه در نجوم، معماری و حتی طراحی گرافیکی استفاده میشود.
